| 一問一答クイズ [No.10014] | |
|---|---|
|
|
|
|
|
|
| 制限時間 : 無制限 | |
| 難易度 | |
| 出題数 | 2744人中 |
| 正解数 | 1891人 |
| 正解率 | 68.91% |
| 作成者 | ちゃっかーず (ID:99) |
| 最高連続正解数 | 0 問 |
| 現在の連続記録 | 0 問 ※ユーザーの方は記録が更新されます |
- 1. クイック掛け算検定
- 2. 数列クイズ
- 3. クイック足し算検定
- 4. おつりはいくらテスト
- 5. 中1 数学の基礎?
- 6. クイック引き算検定
- 7. けーさんけんてー
- 8. 数学雑学クイズ
- 9. 素数検定(初級編)
- 10. 全問正解間違いなしクイズ
- 11. クイック割り算検定
- 12. 中1で習う数学 その一
- 13. 簡単な算数
- 14. 算数トレーニング(小学生)
- 15. 計算&算数クイズ
- 16. クイックマイナス算
- 17. 算数ニコニコ検定
- 18. 計算検定10級(小1レベル)
- 19. 数列穴埋めクイズ
- 20. 確率問題
すぐに答えを見たい場合は「解答を表示する」をクリックしてください。
こちらで学習をして、このクイズ・検定の合格を目指しましょう!
解答を表示する
正解:④
解答を表示する
正解:②
解答を表示する
正解:①
解答を表示する
正解:①
解答を表示する
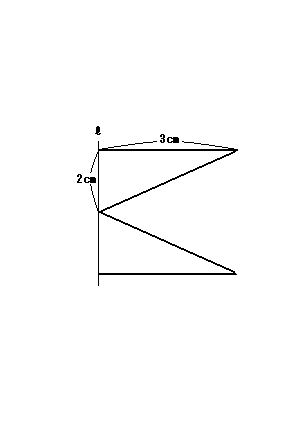
正解:①
解説:回転体の公式(底面積×高さ)で、円錐の体積はこれを3でわると出てくるので、 3×3×π×2÷3=6π・・・? ?が2個あるので、 A.12cm3(立方センチメートル)
解答を表示する
正解:④
解答を表示する
正解:④
解答を表示する
正解:180度×(n-2)
解答を表示する
正解:④
解答を表示する
正解:対角線×対角線÷2
解答を表示する
正解:④
解説:2sinθcosθはsin2θと同値です。
解答を表示する
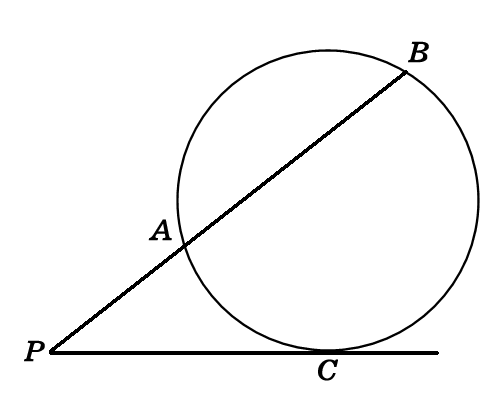
正解:③
解答を表示する
正解:①
解説:グラフを書いてみれば納得できるでしょう 。
解答を表示する
正解:④
解説:6の41乗の常用対数をとれば、x=10により、41(logx2+logx3)=41(0.3010+0.4771)=31.9021となり、31<logx6の41乗<32より、32桁と解ります。
解答を表示する
正解:①
すぐに答えを見たい場合は「解答を表示する」をクリックしてください。
解答を表示する
正解:④
解説:大小の出目の総数は6×6で36通り。うち、大小同じになる確率は6通り。 大小出目が異なるのは36-6で30通りになり、うち半分が大のほうが大きくなる。結果、15/36
解答を表示する
正解:③
解説:二回で決まるということは、あいこになってはいけないということ。 三人でジャンケンをする場合、 Aが(勝ち負けに関わらず)仲間外れになると仮定する。 Aがグーを出した時、B、Cが揃ってパーを出す確率は1/9 B、Cが揃ってチョキを出す確率は1/9で、合わせて2/9。 B、Cが仲間外れになる確率も2/9 なので2/3でひとり勝者、または敗者が決まる。そして、ふたりでじゃんけんをした場合、一回で決着がつく確率は2/3なので、4/9で二回で決着がつく。
解答を表示する
正解:②
解説:玉を全て別物と考えたとき、玉は12C3=12・11・10/3・2・1=220通り うち、赤い玉2個は10C2=45通り、白い玉は2通り、かけて90通り なので90/220=9/22
解答を表示する
正解:5/12
解説:最初、右側にいっても上側にいっても確率は等しいので、右側にいったとして計算する。次の分かれ道を上にいった場合、左にいったらいけない、右か上にいけばいい。そして、上にいったら右、右にいったら上にいけばゴールなので、 1/2×2/3×1/2=1/6。 分かれ道を右に行った場合、次の分かれ道を上にいけばいいので1/2×1/2=1/4。 1/6+1/4=5/12
解答を表示する
正解:②
解説:サイコロを3回振った時、12以上になる確率を求める。 サイコロ3回ふったときの出目は6×6×6で216通り。 一度でもふりだしに戻ればゴールできない。 1〜5のみで12以上になるのは、 2・5・5 3・4・5 3・5・5 4・4・4 4・4・5 4・5・5 5・5・5 全部バラバラ=1通り ふたつ同じ=4通り 全部同じ=2通り 全部バラバラなら3!=3×2×1=6通り。 ふたつ同じなら3C2=3通りに分類できるので、 1×6+4×3+2×1=6+12+2=20 20/216=5/54
解答を表示する
正解:①
解説:5人でジャンケンをした場合の組み合わせは3の五乗で243通りある。 5人がチョキとパーを出す組み合わせを計算する。 5人がチョキかパーを出す組み合わせは2の五乗で32通り。そのうち、全員がチョキ、パーならあいこになるので、32-2=30がチョキとパーの組み合わせ。 グーとパー、グーとチョキの組み合わせも等しいので、90通り。 90/243=10/27となる。
解答を表示する
正解:①
解説:表と裏が等しく出る確率は、10C5/2^10。 252/1024=126/512 つまり、表と裏が等しくない確率は、386/512 そのため、表の方が大きくなる確率はその半分、193/512となる
解答を表示する
正解:②
解説:サイコロの一個目と二個目が等しくなる確率は1/6、さらにもうひとつ同じになる確率は1/6なので、かけて1/36
解答を表示する
正解:③
解説:全部裏の場合、表の枚数は0になるからサイコロの目と等しくなることはない。 そのため、全部裏にならない確率を計算する。 1-1/8=7/8。そして、表が1枚であろうと2枚であろうと3枚であろうと、サイコロの目が出る確率は1/6なので、7/8×1/6=7/48
解答を表示する
正解:①
解説:1回目、Aが勝つ確率は1/3 あいこの後にAが勝つ確率は1/3×1/3 あいこの後にさらにあいこが続き、最後にBに負けない確率は1/3×1/3×2/3 1/3+1/9+2/27=14/27
解答を表示する
正解:①
解説:こういうくじ引き問題は、一人目であろうと100人目であろうと等しい確率で出る。玉は合計101個あるので1/101。
解答を表示する
正解:③

