| 一問一答クイズ [No.30629] | |
|---|---|
|
|
|
 |
|
| 制限時間 : 無制限 | |
| 難易度 | |
| 出題数 | 414人中 |
| 正解数 | 389人 |
| 正解率 | 93.96% |
| 作成者 | KSNK (ID:16885) |
| 最高連続正解数 | 0 問 |
| 現在の連続記録 | 0 問 ※ユーザーの方は記録が更新されます |
- 1. おつりはいくらテスト
- 2. 円周率検定
- 3. 公式・方程式検定
- 4. 掛け算検定。
- 5. 素数検定(初級編)
- 6. 中1 数学の基礎?
- 7. 偏差値検定
- 8. 中1で習う数学 その二
- 9. 数列クイズ
- 10. 中1で習う数学 その一
- 11. 英数理社国 クイズ
- 12. 数学3級検定
- 13. 「い」のクイズ
- 14. 文字式テスト
- 15. 数学雑学クイズ
- 16. 四則記号
- 17. 全問正解間違いなしクイズ
- 18. 暗算6級問題
- 19. 算数トレーニング(小学生)
- 20. 超簡単たし算クイズ
- 1. 中学5教科クイズ
- 2. 理科のクイズ
- 3. 日本の数字の単位検定
- 4. 計算検定(激ムズ)
- 5. くいっく九九検定
- 6. けーさんけんてー
- 7. 引き算クイズ!
- 8. すぴーど算数検定
- 9. 科学なんでもクイズ
- 10. 九九検定81題 順番
- 11. 数学記号試験
- 12. 定理名検定
- 13. ★ 17,18,19段のかけ算
- 14. 2400検定
- 15. ★ 15,16段のかけ算
- 16. 10ケタ×10ケタのかけ算検定
- 17. クイズ計算_ノウハウ
- 18. 2年生までのごちゃ混ぜテスト
- 19. Aの導きクイズ
出題文をクリックするとクイズにチャレンジできます。
すぐに答えを見たい場合は「解答を表示する」をクリックしてください。
こちらで学習をして、このクイズ・検定の合格を目指しましょう!
すぐに答えを見たい場合は「解答を表示する」をクリックしてください。
こちらで学習をして、このクイズ・検定の合格を目指しましょう!
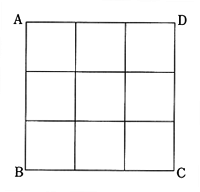
①70度
②6通り
③12通り
④22通り
解答を表示する
正解:④
①0
②24通り
③24
④16
解答を表示する
正解:④
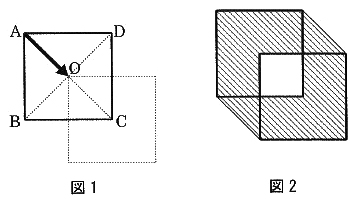
①1260c?
②32
③1575c?
④1675c?
解答を表示する
正解:③
①24番目
②1758c?
③52番目
④56番目
解答を表示する
正解:12番目
解説:1番目→1×2−1=1個 2番目→2×2−1=3個 3番目→3×2−1=5個 4番目→4×2−1=7個 ・・・・・ 10番目→10×2−1=19個 1番目まで→1×1=1個 2番目まで→2×2=4個 3番目まで→3×3=9個 4番目まで→4×4=16個 ・・・・・ 144=12×12 なので、12番目

①160
②12番目
③193
④200
解答を表示する
正解:③
解説:( 3×3×3.14×90/360+4×4×3.14×90/360 +5×5×3.14×150/360 + 3×4) × 3 ={( 9/4+4+125/12 )×3.14 +12}×3 =(200/12 ×3.14 +12)×3 =157+36 =193(c?) となります。

①2
②4
③6
④7
解答を表示する
正解:①
解説:?+?+?+?+?+?=6+7+5=18c? なので、 ?+?+?=18÷2=9c? ?=9−7=2c?
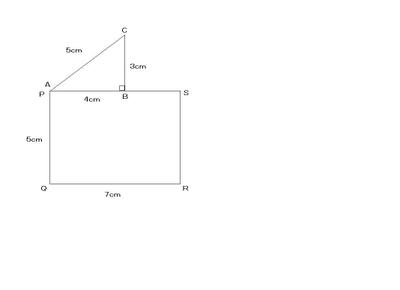
①255
②52.4
③54.1
④57.6
解答を表示する
正解:③
解説:360x2−(90x3+60x2)=330度と求められる。 よって、求める外周の合計は、 左上の半径4cm、中心90度の扇形の弧+ 半径5cm、330度扇形の弧 +直線部分 =2x4×3.14x90/360+2x5×3.14x330/360+19 =25.12+28.78+19=54.1cm(答)
①64.3
②4.5%
③0.045%
④0.45%
解答を表示する
正解:②
①10.00:0.7
②1.0:7.0
③10:7
④1:7
解答を表示する
正解:③
このクイズ・検定や問題に関連するクイズを出題しております。出題文をクリックするとクイズにチャレンジできます。
すぐに答えを見たい場合は「解答を表示する」をクリックしてください。
すぐに答えを見たい場合は「解答を表示する」をクリックしてください。
以下のクイズは、超簡単たし算クイズより、出題しております。
説明:小学1年生でもできる足し算クイズです。
①304
②333
③309
④45%
解答を表示する
正解:308
①4
②2
③1
④308
解答を表示する
正解:②
①49
②33
③68
④69
解答を表示する
正解:③
①11
②3
③3
④9
解答を表示する
正解:10
①15
②12
③10
④19
解答を表示する
正解:②
①29
②33
③18
④28
解答を表示する
正解:①
①10
②8
③9
④30
解答を表示する
正解:③
①11
②18
③38
④37
解答を表示する
正解:④
①7
②19
③8
④9
解答を表示する
正解:③
①15
②13
③6
④12
解答を表示する
正解:②
①24
②50
③74
④11
解答を表示する
正解:③
解説:正解は 74 です
①2490
②2500
③1000
④1490
解答を表示する
正解:①
解説:正解は 2490 です
①8
②70
③9
④7
解答を表示する
正解:④
解説:正解は 7 です
①10
②1
③4
④2
解答を表示する
正解:3
①2
②6
③3
④5
解答を表示する
正解:②
①9
②11
③12
④10
解答を表示する
正解:④
①9
②5
③7
④3
解答を表示する
正解:8
①8
②3
③7
④4
解答を表示する
正解:11
①15
②11
③18
④10
解答を表示する
正解:12
①12
②7
③3
④5
解答を表示する
正解:8

